Driver: Begin¶
Within the FIREBALL program suite [1], slightly excited numerically generated pseudo-atomic fireball wave-functions (also known as Sankey-Niklewski wave-functions) are used. The BEGIN module generates these wave-functions by solving the Schrödinger equation for the free atom with the given boundary condition that the wave-function goes to zero at some radial cutoff (rc). These routines also generate the neutral atom potentials and the Coulombic shell potentials required for the CREATE module (which generates the Hamiltonian interactions).
In solving the one-electron Schrödinger equation,
a set of slightly excited pseudo-atomic fireball wave-functions are computed within density-functional theory (using either the local-density approximation or generalized gradient corrections) and a norm-conserving separable pseudo-potential [2] and are chosen such that they smoothly vanish at the cutoff radius.
This cutoff boundary condition is equivalent to an atom in the box and has the effect of raising the electronic energy levels (i.e., the atomic eigenvalues) due to atom confinement (e.g. Fermi compression of the atom). The radial cutoffs are chosen such that the electronic energy levels remain negative (bound states) and are mildly perturbed from the free atom, and given excitation energies are used to determine the radial cutoffs. Typically, the excitation energy of choice is 0.15 Ryd above the energy of the free-atom. However, for molecules or systems where longer-ranged interactions should be considered, then an excitation choice of 0.10 Ryd is better.
Figure 1 shows a comparison between fireball wave-functions and free-atomic wave-functions (s- and d-state for Au). It is very important that the radial cutoffs are chosen to preserve the chemical trends of the atoms; the excitation of the atoms must be done in a manner that preserves the relative ionization energies and relative atomic sizes. A theoretical basis for judiciously choosing the the radial cutoffs is discussed in Ref. [3] . For this example of the two Au valence states, an excitation energy of ~ 2.0eV (or 0.15 Ryd) yields the following radial cutoffs rc5d = 4.7 aB and rc6s = 5.0 aB. Note, that for the Au d-state, there is not a noticeable distinction between the exact wavefunction and the wavefunction with rc5d = 4.7 aB (d-states are more contracted).
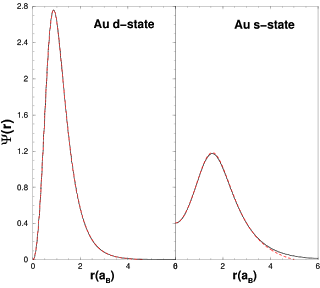
Figure 1. The slightly excited pseudoatomic orbitals for the d-state and s-state of Au (solid line: free-atomic wavefunction, dashed line: fireball wavefunctions).
The fireball boundary condition yields two promising features that enable computationally efficient calculations. First, the range of hopping matrix elements between orbitals on different atoms is limited; therefore, very sparse matrices are created for large systems. This inherent sparseness allows one to more readily implement linear-scaling algorithms to obtain the band structure energy. Second, the slight excitation of the atoms somewhat accounts for Fermi compression in solids which present a better representation of solid-state charge densities [3] .
A flexible choice of basis set where double numerical or additional polarization sets are permitted within FIREBALL. Earlier work shows that the addition of the double numerical basis set yields comparable results to other ab initio tight-binding methods given in Refs. [4] and [5] .
In addition to the wave-functions, the BEGIN module creates the neutral atom and charged atom potentials (i.e., Hartree interactions). The neutral atom potential is determined from
The charged atom potential is based on the wavefunction of the shell, so the piece for the s-shell is determined by
These Hartree potentials are required for calculating Coulombic matrix elements in the CREATE module.
Running the BEGIN Module¶
5.0 Some notes about exchange-correlation¶
| Enumeration of exchange-correlation approximations. | ||
|---|---|---|
| Number | Limit | Exchange-Correlation Type |
| 1 | LDA | Wigner |
| 2 | LDA | Hedin/Lundqvist |
| 3 | LDA | Ceperley/Alder Perdew/Zunger (1980) |
| 4 | GGA | Perdew/Wang (1991) |
| 5 | GGA | Becke (1988) X, Perdew (1986) |
| 6 | GGA | Perdew/Burke/Ernzerhof (1996) |
| 7 | LDA | Zhao/Parr |
| 8 | LDA | Ceperley/Alder Perdew/Wang (1991) |
| 9 | GGA | Becke (1988) X, Lee/Yang/Parr (1988) |
| 10 | GGA | Perdew/Wang (1991) X, Lee/Yang/Parr (1988) |
| 11 | LSDA | Volko/Wilk/Nusair (1980) |
| 12 | B3LYP | BLYP (9 GGA) with exact exchange |
Table 1↓ lists the different exchange-correlation options; note that only option ‘3’ and option ‘9’ are currently programmed within the FIREBALL suite of codes. Table 1
5.1 Building the executables¶
All packages are stored in the svn repository.
First, checkout /fireball-thunder and /fireball-begin from the svn repository at https://fireball.phys.wvu.edu/svn/THUNDER (you will need a user account on our server to download).
Note that all the modules for running the new suite of FIREBALL codes are found in /fireball-thunder/src. Generally, only the drivers are found in other sub-directories and symbolic links are made to /fireball-thunder/src sub-directories. This strategy is chosen so that all FIREBALL codes will now utilize common modules throughout future versions.
You will then need to go to /fireball-begin/src and type ./runme_before_compile.sh. Note that there is a single common Makefile for creating all FIREBALL codes. Check this Makefile before creating any executables. For example, make sure that the correct MACHINE file is chosen in the Makefile (you may need to build your own MACHINE file). Also, in the Makefile - choose the correct XC (exchange-correlation) flag (currently the two flags available are XC = LDA for exchange-correlation option 3 and and XC = BLYP for exchange-correlation option 9).
Once these steps are finished you are ready to make the executables that are necessary for running fireball-begin: begin.x and begin-looprc.x. To make these, type make begin.x and make begin-looprc.x to create the executables.
Before running begin.x and begin-looprc.x, there are two important components that must be added: the pseudo-potential files and the input files. These need to be added to specific sub-directories.
5.2 Getting started - setting up the sub-directories and pseudo-potential files¶
First we will set up the directories for the pseudo-potentials and input files.
For setting up the directories, the following guidelines are followed. First, make a sub-directory name of the element under /fireball-begin, i.e., /N for nitrogen (assuming that a sub-directory does not yet exist). Second, make a sub-sub-directory with a number signifying which exchange-correlation option is used and which valences are used for the pseudo-potentials. Hence, /fireball-begin/N/3.s2p3.p1p2 signifies that we are generating wave-functions for nitrogen, using LDA option ‘3’, the first pseudo-potential has a valence of 2 and 3 in the s- and p-states, respectively, and, in this case, we use valence states of 1 and 2 for the s- and p-states, respectively, for the second, excited-state, pseudo-potential. Note, in principle, the pseudo-potentials are transferable and the 007.s2p3.pp can be used for both ground- and excited-states; however, we generally choose to utilize the excited-state pseudo-potential to generate the excited state wave-functions for convenience (more on this later).
Psuedo-potential files: Next, create the sub-directory /fireball-begin/N/3.s2p3.p1p2/Fdata/basis. For convenience with using all FIREBALL codes, all pseudo-potentials are stored in the input sub-directory /Fdata/basis and all wave-functions are output to the same sub-directory. Many pseudo-potentials have already been created and are found in the PPfiles sub-directories under /fireball-begin, e.g. /fireball-begin/N/Ppfiles. For example, for nitrogen - there exist the sub-directory /fireball-begin/N and there are the following sub-directories: /3.s2p3.p1p2, /9.s2p3.s1p2, and /Ppfiles. The nomenclature for the naming scheme of the psuedo-potential files is in the form Z.snpm.pp, where Z is the atomic number (e.g., 014 for Si) and the numbers n and m signify the occupation valence for the s- and p- states respectively (for example, the pseudo-potential for nitrogen using LDA, option ‘3’, is stored in /fireball-begin/N/PPfiles/3/007.s2p3.pp). Note that the sub-directories under /PPfiles signify the type of exchange-correlation interaction used as specified by the pseudo-potential package, so that, option ‘3’ signifies the local-density approximation of the Ceperley-Alder form [6] as parameterized by Perdew and Zunger [7], option ’9’ signifies Becke exchange [8] with Lee-Yang-Parr correlation [9], etc. Also note that the next module of the FIREBALL package, CREATE, will run with only LDA option ‘3’, or the GGA-BLYP option, e.g., option ‘9’, for the exchange-correlation interactions. Currently, the other exchange-correlation options are not available in the FIREBALL code. More details about the contents of these sub-directories will become obvious later after thoroughly reading this tutorial. Additionally, wave-functions and pseudo-potentials can also be downloaded on this webpage (coming soon). If the necessary pseudo-potential does not exist, then run the PP package to generate the needed pseudo-potential file.
Hence, copy the files /fireball-begin/N/PPfiles/3/007.s2p3.pp and /fireball-begin/N/PPfiles/3/007.s1p2.pp to /Fdata/basis/007.pp and /Fdata/basis/007++.pp. The executables begin.x and begin-looprc.x are expecting the two pseudo-potential files to be stored in default names 007.pp and 007++.pp. Note that the ‘++’ generally signifies that the excited state wave-functions are generated from the 2+ ion; however, in some cases, a different ion is used or the ground-state pseudo-potential can be used to generate the excited states. Regardless, the pseudo-potential used to generate the excited states is still stored in the file Z++.pp.
5.3 Finding the cutoffs - begin-looprc.x¶
The first step towards generating fireball wave-functions is to determine the necessary cutoffs. Typically, the cutoffs should be chosen such that the energy of the new fireball pseudo-atomic orbital is 0.15 Ry above the energy of the free-atom (the infinite cutoff case). This has been historically determined to be the criteria of choice, because the cutoffs given by this excitation energy provide enough neighbor interactions in the Hamiltonian to produce a sufficiently accurate cohesive energy in bulk materials (in Si the error is 10 − 5 compared to the cohesive energy calculated with infinite cutoffs). In hydrogen-bonded systems it is advisable to decrease the criteria for the excitation energy to 0.10 Ry. With this latter criteria, the cutoffs in general will be about 10% longer and the fireball wave-functions should be extended about 10% longer for hydrogen-bonded systems.
The program begin-looprc.x will loop through different cutoffs so that the ideal cutoffs for the fireball wave-functions may be determined.
Before we can run begin-looprc.x three files need to be created: Fdata.inp, looprc.inp, and Z-looprc.inp (where Z is the atomic symbol). The template for each of these files are as follows,
Fdata.inp
1 ! Number of species
7 ! Atomic number (list line by line according to number of species)
Fdata ! Location of the Fdata input/output (generally symbolically linked to /Fdata)
looprc.inp
James P. Lewis ! Name of the person running begin-looprc.x
N-looprc.inp ! Name of the input file for the species (list line by line; number of species)
So, in principle, begin-looprc.x can be run for more than one species. To run for multiple species, merely change the number in the Fdata.inp file and add the appropriate pseudo-potential files to /Fdata/basis. If multiple species are calculated, then make a Z-looprc.inp for each species, as follows:
N-looprc.inp
Nitrogen ! atom name
N ! atom symbol
7 ! atomic number
14.007 ! atomic mass
5.0 ! number of valence electrons
3 ! exchange-correlation option
2 ! number of shells
0 ! angular momentum of shell 1
2.0 ! number of electrons in shell 1
1 ! angular momentum of shell 2
3.0 ! number of electrons in shell 2
3.0 ! initial radial cutoff
8.0 ! final cutoff
12.0 ! infinity radial cutoff - to get free atom eigenvalues
Note that as a general rule when running begin-looprc.x and begin.x for transition metals: The p-state is included even though the p-state is empty for transition metals. So for instance, a Z-looprc.inp file for a transition metal might look something like.
Au-looprc.inp
Gold ! atom name
Au ! atom symbol
79 ! atomic number
196.967 ! atomic mass
11.0 ! number of valence electrons
3 ! exchange-correlation option
3 ! number of shells
0 ! angular momentum of shell 1
1.0 ! number of electrons in shell 1
1 ! angular momentum of shell 2
0.0 ! number of electrons in shell 2
2 ! angular momentum of shell 3
10.0 ! number of electrons in shell 3
3.0 ! initial radial cutoff
8.0 ! final cutoff
12.0 ! infinity radial cutoff - to get free atom eigenvalues
Note that for transition metal atoms, we typically keep the empty p-state at all stages for polarization.
With these files in the directory, run the program (type ./begin-looprc.x) and follow the instructions and answer the questions given by the execution of the code. Note that the necessary pseudo-potential file must be available in the running directory or begin-looprc.x will crash.
The output of begin-looprc.x will be written to an output.log file and a Z.eig file, where Z indicates the atomic number of the atom (e.g. for N, the file name would be 007.eig). The output.log file is merely the “screen” output from the program. Table 2 shows an example of the the type of information found in the 007.eig file. Listed for each shell, the output contained in the Z.eig file are (in order) the cutoff, the energy eigenvalue for that cutoff, and the energy difference (delta) between the energy eigenvalues of the free atom and the fireball atom. The information is listed in order of shell (for flexibility, different cutoffs are presumed for each shell).
Table 2 An example of the type of information found in file 007.eig after running the looprc.x program.
SHELL 1 SHELL 2
rc eigen delta rc eigen delta
3.000 -0.88595 0.46830 | 3.000 0.00654 0.53901
3.000 -0.89954 0.45472 | 3.050 -0.02004 0.51243
⋮ ⋮ ⋮ | ⋮ ⋮ ⋮
3.650 -1.20093 0.15332 4.050 -0.37279 0.15968
3.650 -1.20604 0.14822 4.100 -0.38007 0.15240
3.650 -1.21092 0.14333 4.150 -0.38696 0.14551
⋮ ⋮ ⋮ | ⋮ ⋮ ⋮
3.750 -1.25210 0.10215 | 4.500 -0.43514 0.09733
3.800 -1.18590 0.16835 | 3.800 -0.33801 0.19446
⋮ ⋮ ⋮ | ⋮ ⋮ ⋮
4.850 -1.33066 0.02360 | 5.600 -0.50832 0.02415
4.900 -1.30853 0.04573 | 4.900 -0.48121 0.05126
⋮ ⋮ ⋮ | ⋮ ⋮ ⋮
You will need a python script called Glean.py which is located in /fireball-begin/src. The script Glean.py will choose the best 5 cutoff values from the Z.eig file. Run the script by typing python Glean.py. If you need more information, add the - - help flag. When working with transition metals, you will need to add the flag –ignorep. From this list you will need to choose values such that the difference between the two cutoffs is approximately Δrc = 0.4aB (a general rule of thumb). The cutoffs need be chosen in a way that the energy difference between the energy eigenvalues of the free atom and the fireball atom is the same for all shells. If not, then the excitation energies for each shell will be raised in a way that will not preserve the chemical trends of the atoms. Glean.py will preserve the chemical ordering of the eigenvalues when executed.
5.4 Calculating the wave-functions - begin.x¶
Before running begin.x two more files need to be created: begin.inp and N-begin.inp (where N is the atomic symbol). The template for each of these files are as follows,
begin.inp
James P. Lewis ! Name of the person running begin.x
N-begin.inp ! Name of the input file for the species (list line by line; number of species)
So, in principle, begin.x can be run for more than one species. To run for multiple species, merely change the number in the Fdata.inp file and add the appropriate pseudo-potential files to /Fdata/basis. If multiple species are calculated, then make a Z-begin.inp for each species, as follows:
N-begin.inp
Nitrogen ! atom name
N ! atom symbol
7 ! atomic number
14.007 ! atomic mass
5.0 ! number of valence electrons
3 ! exchange-correlation option
3 ! number of shells (add three lines for each shell)
0 ! angular momentum of shell 1
2.0 ! number of electrons in shell 1
3.80 ! radial cutoff for shell 1
1 ! angular momentum of shell 2
3.0 ! number of electrons in shell 2
4.45 ! radial cutoff for shell 2
2 ! angular momentum for shell 3 (this is an empty polarization state)
0.0 ! number of electrons in shell 3
4.45 ! radial cutoff for shell 3
1 ! use excited states (do not include the "excited" lines if set to 0)
2.0 ! number of valence electrons (excited)
1.0 ! number of electrons in shell 1 (excited)
2.0 ! number of electrons in shell 2 (excited) (one line for each shell above)
0.0 ! number of electrons in shell 3 (excited)
1 ! optimize basis set with confinement potential
0.0 ! Vo for shell 1
0.0 ! r0 for shell 1
0.0 ! V0 for shell 2 (two parameters for each shell listed above)
0.0 ! r0 for shell 2
20.0 ! V0 for shell 3
0.0 ! r0 for shell 3
100.0 ! V0 for shell 1 (excited)
0.0 ! r0 for shell 1 (excited)
200.0 ! V0 for shell 2 (excited)
0.0 ! r0 for shell 2 (excited)
0.0 ! V0 for shell 3 (excited)
0.0 ! r0 for shell 3 (excited)
There are several output files for begin.x; first, the screen output will be stored in output.log. Second, a file for create.x will be automatically created for each atom included, for example, for nitrogen, N-create.inp will be a generated output file from begin.x. The Z-create.inp file is input file for create.x. In addition to this output, there will be output of the fireball wave-functions (e.g., 007_380.wf1), the neutral atom potential (e.g., 007_445.na0), and the Hartree potentials for each shell (e.g., 007_380.na1). This output will be stored in /Fdata/basis. The files are named according to the parameters listed in the Z-begin.inp. The first number in the file nomenclature is the atomic number, the second number is the radial cutoff, so that 3.80 is represented by 380, and the suffix is the type of file (wf = wavefunction and na = Hartree potential). Hence, 007_380.na1 is the Hartree potential for the first shell (s-state) of nitrogen (007) with radial cutoff 3.80 (380).
5.5 Excited states and polarization states¶
We follow the DMOL formalism for developing excited numerical states, as outlined in Ref. [10]. This involves generating the wave-functions for the 2+ ion (or generally any + ion can be used) and then orthogonalizing the wave-functions of this ionized atom to the original ground state wave-functions. This algorithm is now fully automatic within the BEGIN module by choosing ‘1’ in the line - ”! use excited states”. Make certain that the pseudo-potential for the ionized atom is copied to the file Z++.pp (e.g., 007++.pp for the 2+ ion of nitrogen) in /Fdata/basis.
Note that hydrogen is a special case when generating the DMOL basis set, because there is no such thing as a 2+ ion for the atom. Currently, the BEGIN module cannot do this for hydrogen, although one could just generate an excited wave-function of the ground state atom by just copying the 001.pp pseudo-potential file to the 001++.pp file; do not generate a separate pseudo-potential file.
Polarization wavefunctions (for example, a d-state on nitrogen) can be easily generated by listing an extra shell (for example, in the case of nitrogen, by choosing ‘3’, rather than ‘2’, in the line - ”! number of shells”).
5.6 Optimized wave-functions¶
The code begin.x provides a way to generate an optimized state wave-function based on application of extra confinement potential. The confinement potential is defined as:
For details, see Ref. [11].
5.7 Plotting the results¶
The output files are in a form that can be readily plotted. It is always wise to plot the wavefunctions to insure that they look reasonable and to avoid problems later. The data for plotting purposes are contained in the following files - sstate0, sstate1, pstate0, pstate1, ..., etc. for the wavefunctions and NA_plot, NA_splot, NAe_splot, NA_pplot, NAe_plot, ..., etc. for the neutral (charged) atom potentials. For the wavefunction files, the ’0’ signifies wavefunctions for the ground state and ’1’ signifies wavefunctions for the excited states. Similarly, the ’e’, i.e. NAe_splot, signifies that the file contains neutral (charged) atom data for the excited state.
Acknowledgements¶
This research was funded in part by: The University of Utah Center for the Simulation of Accidental Fires and Explosions (C-SAFE), funded by the Department of Energy, Lawrence Livermore National Laboratory, under subcontract B341493; Department of Energy, Basic Energy Sciences, grant No. DE-FG02-03ER46059; National Science Foundation, Information Technology Research, grant No. CHE-0326027.
References¶
| [1] | J.P. Lewis, P. Jelínek, J. Ortega, A.A. Demkov, D.G. Trabada, B. Haycock, H. Wang, G. Adams, J.K. Tomfohr, E. Abad, H. Wang, and D.A. Drabold. “Advances and applications in the FIREBALL ab-initio tight-binding molecular-dynamics formalism,” Phys. Stat. Sol. B., 248, 1989-2007 (2011). |
| [2] |
|
| [3] | (1, 2) O.F. Sankey, A.A. Demkov, W. Windl, J.H. Fritsch, J.P. Lewis, and M. Fuentes-Cabrera. “The application of approximate density functionals to complex systems,” J. Quant. Chem., 69, 327-340 (1998). |
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] | M.A. Basanta, Y.J. Dappe, P. Jelínek, and J. Ortega. “Optimized atomic-like orbitals for first-principles tight-binding molecular dynamics,” Comp. Mat. Sci., 39, 759–766 (2007). |
The Begin driver is composed of two executables begin.x and begin-looprc.
The purpose of the driver is to compute the atomic wave-functions that will be
used by the driver Create to compute the interatomic interactions and by the
driver Fireball to compute the electronic structure.