Driver: Create¶

4 Introduction¶

4.1 Pre-computing the interactions¶

For a full theoretical discussion of the multi-center interactions created within FIREBALL see Ref. [1] and references therein. Given any two atomic orbitals, i and j, beyond some cutoff interaction distance (\(r_{ci}\) + \(r_{cj}\)) the matrix elements \(H_{ij}\) and \(S_{ij}\) become exactly zero; for example, an overlap matrix element of two s-orbitals is demonstrated in Fig. 1. As a result of these cutoff distances, there is only a prescribed interaction range over which the integrals need be evaluated; outside of the cutoff distance all interactions are exactly zero (except long-range coulomb). It’s worthwhile to mention, in the case of pseudopotential integrals, it is used different cutoff radius \(r_{c}^{PP}\) related to pseudoatomic wavefunction \(\Psi^{NL}\). Then the pseudopotential integrals become exactly zero beyond certain distance (\(r_{ci}\) + \(r_{cj}^{PP}\)).

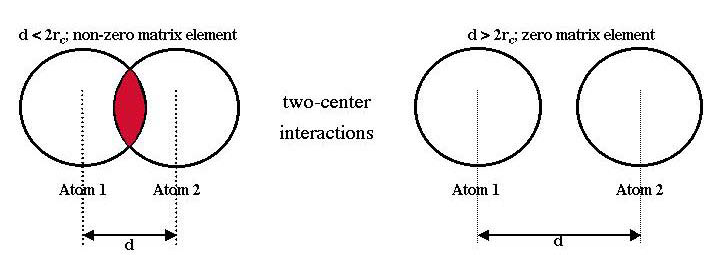
Figure 1. The two-center interaction: due to cutoffs (rc) used in the method, the interaction range (d) of two s-orbitals, shown here, is non-zero only within some finite range.

Within the FIREBALL approach, all integrals may be pre-computed on a numerical grid and the specific values needed are gleaned from the tabulated values via interpolation. With this approach, interactions calculated within the CREATE module will be readily available. For two-center interactions, a cubic spline function is chosen as the interpolation method, so as to maximize numerical stability. Because these integral tables depend only on the atom type, their rc values, and the type of DFT exchange-correlation functional chosen, the integral tables only need to be generated once, for a given set of atomic species. As long as the criteria chosen for generating the data files does not change (such as choosing a different exchange-correlation functional), the data files may be used over and over again, saving overall computation time.

The other two traditional approaches to integral evaluation were rejected for efficiency reasons. Within the “conventional” approach employed, such as the algorithms implemented in gas-phase electronic-structure codes, integrals are evaluated once per geometry and stored to disk for use during the SCF procedure. This approach results in extensive disk I/O and computation. The “direct” approach in which integrals are calculated as needed is similar to the approach taken within FIREBALL. Given the large computational cost of calculating each individual integral (because the integrals are evaluated numerically), the evaluation of different matrix element components are performed via interpolation within FIREBALL, rather than via explicit evaluation of the integral as done in the gas-phase direct approach.

4.2 Parallel scalability¶

The generation process for the atomic interactions lends itself to easy parallelization by spreading the data file creation over multiple processors based on differing integral types. Within the CREATE module, integrals are distributed to different processors based upon atomic number and based upon integral type (kinetic, overlap, exchange-correlation, etc.). The simple loop based approach is used for distributing work to processors and has been found to be very effective. This approach minimizes communication while distributing work evenly across the processors. This parallelization scheme is particularly important, since the number of data files needed grows as O(M3) with the number of different atomic species M.

4.3 Three-center interactions¶

The three-center interactions are calculated according to a bond-charge scheme; the three-centers define the π - σ plane (see Fig. 2). The σ axis is the axis connecting the two orbitals μ and ν forming the bond charge, and the origin is midway between the two orbitals. The origin lies at the bond-charge center, equidistant from the two atoms forming the bond charge. The bond charge interaction, defined by the bond-charge distance (dBC), is non-zero only in the region of intersection of the two spheres of radius rc. The non-zero three-center integrals are written in the following form:

\[V_{\mu\nu}(d, d_{BC}, \theta) = \langle \phi_{\mu}^{PAO} (\vec{r} + \frac{1}{2} d_{BC} \sigma |V(\vec{r} - \vec{d})| \psi^{PAO} (\vec{r} - \frac{1}{2}d_{BC} \sigma)) \rangle\]

The kernel is expanded in associated Legendre polynomials P nm(cos \(\theta\)) in the standard way. We truncate the series after n = 4, so for each relevant value of \((\mu, \nu)\) we have at most five functions, \(q_0, q_1, q_2, q_3,\) and \(q_4\). Each value of n is stored in a separate data file (see Sec. 6). For fixed d and \(d_{BC}\), \(\theta\) is varied over five angles and the interactions are evaluated exactly by performing a three-dimensional integral. We choose the following five angles: \(cos \theta = 0, \sqrt{3}, -\sqrt{3}, \sqrt{3/5},\) and \(-\sqrt{3/5}\). The five functions \(q_n\) at the chosen value of d and \(d_{BC}\) are determined from five equations in five unknowns. The process is repeated over a grid of values of d and \(d_{BC}\) up to \(r_{ci} + r_{cj}\). Past \(r_{ci} + r_{cj}\), the matrix elements must be identically zero.

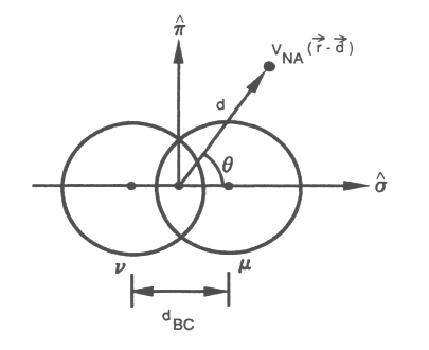
Schematic of the three-center interaction

Figure 2. The three-center interaction. The bond-charge (\(d_{BC}\)) defines the distance between the first two-centers(centers can be defined as wavefunctions or potentials, such that we are calculating matrix elements , and the three-center interaction is non-zero only within some finite range defined by \(d_{BC} < r_{ci} + r_{cj}\). The third center (at \(V_{NA}\) shown) is defined by the angle, \(\theta\), and the distance, \(d\), from the center of the bond charge distance.

5 Running the CREATE Program¶

5.0 Some notes about exchange-correlation¶

Table 1↓ lists the different exchange-correlation options; note that only option ‘3’ and option ‘9’ are currently programmed within the FIREBALL suite of codes. Table 1 Enumeration of exchange-correlation approximations.

Enumeration of exchange-correlation approximations.
Number	Limit	Exchange-Correlation Type
1	LDA	Wigner
2	LDA	Hedin/Lundqvist
3	LDA	Ceperley/Alder Perdew/Zunger (1980)
4	GGA	Perdew/Wang (1991)
5	GGA	Becke (1988) X, Perdew (1986)
6	GGA	Perdew/Burke/Ernzerhof (1996)
7	LDA	Zhao/Parr
8	LDA	Ceperley/Alder Perdew/Wang (1991)
9	GGA	Becke (1988) X, Lee/Yang/Parr (1988)
10	GGA	Perdew/Wang (1991) X, Lee/Yang/Parr (1988)
11	LSDA	Volko/Wilk/Nusair (1980)
12	B3LYP	BLYP (9 GGA) with exact exchange

5.1 Building the executables¶

All packages are stored in the svn repository: https://fireball.phys.wvu.edu/svn/THUNDER (you will need a user account on our server to download). There are two sub-directory downloads that are needed to successfully run create.x; these are /fireball-thunder and /fireball-create. Checkout these two sub-directories from the svn repository. Note that all the modules for running the new suite of FIREBALL codes are found in /fireball-thunder/src. Generally, only the drivers are found in other sub-directories and symbolic links are made to /fireball-thunder/src sub-directories. This strategy is chosen so that all FIREBALL codes will now utilize common modules throughout future versions.

After checking out /fireball-thunder and /fireball-create - go to /fireball-create/src and type ./runme_before_compile.sh - after which you can type make create.x to create the executable. Note that there is a single common Makefile for creating all FIREBALL codes. Finally, before typing make, make sure that the correct MACHINE file is chosen in the Makefile (you may need to build your own MACHINE file). Also, in the Makefile - choose the correct XC (exchange-correlation) flag (currently the two flags available are XC = LDA for exchange-correlation option 3 and and XC = BLYP for exchange-correlation option 9).

5.2 Getting started - setting up the input and output sub-directories¶

Acknowledgements¶

This research was funded in part by: The University of Utah Center for the Simulation of Accidental Fires and Explosions (C-SAFE), funded by the Department of Energy, Lawrence Livermore National Laboratory, under subcontract B341493; Department of Energy, Basic Energy Sciences, grant No. DE-FG02-03ER46059; National Science Foundation, Information Technology Research, grant No. CHE-0326027.

References¶

[1]	J.P. Lewis, P. Jelínek, J. Ortega, A.A. Demkov, D.G. Trabada, B. Haycock, H. Wang, G. Adams, J.K. Tomfohr, E. Abad, H. Wang, and D.A. Drabold. “Advances and applications in the FIREBALL ab-initio tight-binding molecular-dynamics formalism,” Phys. Stat. Sol. B., 248, 1989-2007 (2011).

The Create driver is compose of one executable create.x. The purpose of the driver is to compute the interatomic interactions up to three centers. The interactions are stored in the Fdata directory (old style) or the new HDF5 Fdata.hdf (new style). The driver works with the wave-functions created by the driver Begin and will be used by the driver Fireball to compute the electronic structure.